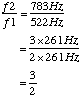Tuning, Scales and Temperament
Harmonic and Inharmonic Spectra
The sounds that we hear from vibrating objects are complex in the sense that they contain many different frequencies. This is due to the complex way that objects vibrate.
A "note" (say Middle C) played on a piano sounds different from the same "note" played on a saxophone. In both cases there are different frequencies present above the common fundamental note sounded. These different frequencies are part of what enables you to distinguish between different instruments. (Their difference in timbre.)
Spectra can be classified as being of one of two types:
(1) Harmonic, in which the spectral components (different frequencies) are mostly whole number multiples of the lowest, and most often loudest, frequency. The lowest tone is called the fundamental and the higher (i.e. in frequency) spectral components, the tones over the fundamental, are called overtones, or harmonics.
(2) Inharmonic, in which the criteria in (1) are not met i.e in which the spectral components are mostly NOT whole number multiples of the lowest frequency, which is often NOT the loudest tone. Many percussion instruments fall into this category.
The Harmonic Series
The harmonic series is a series of frequencies that are whole number multiples of a fundamental. For example, taking the tone Middle C whose fundamental frequency is approximately 261 Hz, the harmonic series on this frequency is:
Hs = f , 2f , 3f , 4f , ......... nf and where f = 261 Hz.,
= 261 Hz , 522 Hz , 783 Hz , 1044 Hz , ................... n x 261 Hz.
This is expressed in musical notation thus:
Note that these notes are 'representing' the tones. The frequencies of the actual
tones are at varying distances from the frequencies of these notes depending on the
tuning system used. In particular the 7th partial (B
in this example) is considerably flat in Pythagorean,
just and equal temperaments (see later).
We can see from the above discussion of the harmonic series, that an interval can be expressed as a ratio of the frequencies of the two tones:
The higher of the two tones (f2) is placed over the lower (f1) because we are considering and upward interval.
Example: For the perfect fifth C - G in the above description,
