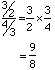
Scales - An Introduction
Throughout history there have been numerous ways devised to divide the octave (frequency ratio of 2/1 sometimes written explicitly as 2:1) into smaller intervals. All the scales[1] thus produced have their own characteristics and are thus more or less suited for the playing of a particular type of music (or particular musics).
Most recent Western music has used a scale with 12 steps - semitone intervals - called the chromatic scale (from the Greek khroma, meaning colour). Other cultures use scales with a different number of steps, for example 4, 5, 7, 11, 12, 13.
Definition of a Musical Scale
A scale is a discrete set of pitch relationships (or intervals), most often arranged in such a way as to yield a maximum possible number of consonant combinations (or minimum possible number of dissonances) when two or more of these intervals are sounded together.
The most consonant interval after the octave is the fifth (3/2) and the next most consonant is the fourth (4/3). The difference between these two intervals
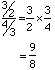
is defined as the interval of a whole-step. This means that in a whole-step interval the frequency of the higher tone is increased by a factor of 9/8 of the lower, or the lower is decreased by a factor of 8/9 of the upper.
Given the restriction on consonance in developing musical scales (see above) we can immediately develop two of the oldest scales, the Pythagorean and the Just.