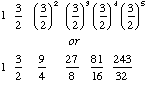
Construction of the Pythagorean Diatonic Scale
The Pythagorean scale is developed from the interval of a perfect 5th.
Step 1: Begin with an arbitrary tone of frequency represented by 1, and ascend in steps of perfect 5ths:
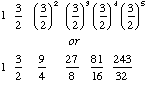
if these were based on C4 the notes would be
C4 G4 D5 A5 E6 B6
Step 2: Reduce the ratios obtained in step 1 into the range of a single octave by descending from these notes in whole octave steps:

Step 3: Arrange the notes obtained in step 2 in ascending order:
![]()
Step 4: The above sequence of notes is missing one important note the one corresponding to a perfect 4th from the beginning point. This can be obtained by descending from the beginning point by a perfect fifth (2/3) and then moving up one octave (2/3) x 2 = 4/3 = 1.3333.... Placing it in the ascending sequence as arranged in step 3, we have the following sequence:
![]()
This is known as the Pythagorean diatonic scale. Examining the intervals between each step,

We can see that the scale consists of the familiar major scale (where the whole step is 9/8 and the 1/2 step is 256/243).
Discussion
Both the perfect 4th and 5th have exact ratios, 3/2 and 4/3 as expected (The scale
was constructed using these intervals.)
The Major 3rd however, is too wide, or sharp. The ratio should be 5/4 = 1.250 but
the Pythagorean scale has this interval as 81/64 = 1.265.
The minor 3rd between the 2nd and 4th degrees should be 6/5 = 1.20 but in fact is
![]() i.e.
it is too narrow, or "flat".
i.e.
it is too narrow, or "flat".