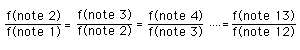
The Tempered Scale
If you start from a particular note and ascend or descend in either perfect fifths or thirds, one never arrives at a note that is a whole number of octaves from the starting note. It is partly this reason that both the Pythagorean and Just scales have posed problems for recent Western musicians (in the last few hundred years). Adjustments have been made to these scales - in the spirit of acoustical compromise - to satisfy three incompatible requirements:
1. True intonation - that is exact thirds, fourths, fifths, etc
2. Complete freedom of modulation - that is from any one key to any other.
3. Convenience in the practical use of keyboard instruments - that is to make it
possible for instruments which have been tuned differently to play together without
retuning.
Equal Temperament
In this form of compromise, the first of these requirements is sacrificed for the good of the latter two requirements. In the equally tempered scale all semitone intervals are exactly the same ratio, irrespective of frequency location. This implies that all whole-tone intervals are likewise equal. In order to accomplish this the octave is divided into twelve equal semitone intervals.
The two criteria then, are
1. That all semitone intervals be identical; i.e.
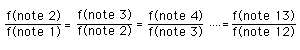
2. That the octave maintain its integrity; i.e.
f(note 13) = 2 x f(note 1)
The first criterion means that the ratio of all the semitone intervals is the same. Call this ratio a.

The ratio of any two semitones is thus the same:
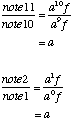
Furthermore, since f(note13) = a![]() f(note 1),
f(note 1),
we have a![]() = 2
= 2
or ![]() a
(12th root of 2)
a
(12th root of 2)
The twelfth root of two is approximately 1.059463094.
Using this fact, the following table shows frequency ratios of intervals within one octave, and gives actual approximate frequencies that result if we begin with Concert A, A4 = 440 Hz (the standard of pitch).

Discussion
The following table allows a comparison between some 12 tone equal temperament and
theoretical ratios:

It is clear from these results that equal temperament mistunes all intervals except the octave. It drastically mistunes thirds and sixths. This results in many intonation difficulties, but in return keyboard instruments can play freely together, scores can be transposed up and down for singers, and compositions using modulations to remote keys can be effected without problems.
Intonation
A competent violinist or vocalist (that rarest of beasts!) plays or sings in an intonation
different from equal temperament when not accompanied by a keyboard instrument. In
a string quartet, for example, the thirds and fourths will be played such that they
sound best, and that is not equal temperament.
An orchestra does not play in equal temperament. Brass players tend to "lip up" or "lip down" certain notes and in doing so depart from equal temperament. The note B in a C major passage is often played sharp in anticipation of a move to the tonic C, whilst the same note B played as the mediant of G major is often played flat relative to the demands of equal temperament.