Analysis of Spectra
Complex Tones
Standing Waves in a String
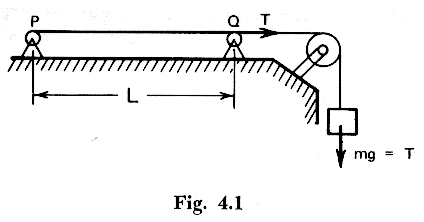
Consider the case of a tense string anchored at fixed points P and Q (figure 4.1) of length L and mass per unit length d, stretched with a given force T that can be changed at will (say by changing the mass m of a body suspended from the string as shown) :
Sympathetic Resonance
Hermann von Helmholtz (1821-1894) Helmholtz resonators - hollow glass spheres that have two short tubular necks, diametrically opposite one another. One opening was put to the ear, the other directed at the sound source. By using a series of these Helmholtz was able to estimate the strengths of the harmonics of a periodic sound. He also found the frequencies of inharmonic partials of bells and gongs.
Resonances have a noticeable effect on the timbre of musical sounds. For brass instruments this is controlled by the length and shape of tubing, and how the player constricts the lips.
For woodwind instruments, their tubular structures are resonators whose resonant frequencies are controlled by opening or closing various holes.
The vocal tract has several resonances that emphasise various ranges of frequency in the sound produced by the vibration of the vocal cords. By changing the shape of the vocal tract, the frequencies of these resonances or formants determine which vowel sound is produced.
The resonances of the soundboard of a violin greatly affect the timbre. The suppression of some partials is important for the musical quality of the violin tone.
Fourier Analysis and Fourier Synthesis
The French Mathematician Baptiste Joseph Fourier (1768-1830) invented a type of mathematical analysis by which it can be proved that any periodic wave can be represented as a sum of sine waves having the appropriate amplitude, frequency and phase. The function that sums all the harmonics into a sound wave is called a Fourier integral. Furthermore for harmonic spectra, the frequencies of the component waves are related in a simple way: they are whole number multiples of a single frequency, f0, 2f0,3f0, and so on.
A square (or pulsed wave with a mark to space ratio of 1:1) requires the sum of an infinite number of sine components whose frequencies are odd whole number multiples of the fundamental (f0, 3f0, 5f0, 7f, ...) and whose amplitudes decrease in proportion to the inverse of the harmonic number (1, 1/3, 1/5, 1/7, ...) and the proper phases.
Most periodic sound waves consist of both odd and even frequency components although closed organ pipes and some wind instruments (eg clarinets) do have predominantly odd frequency components. A triangular wave also has only odd numbered frequency components. Their amplitudes are different to those of a square wave however, reducing to the inverse of the square of the harmonic number (1, 1/9, 1/25, 1/49 ...)
A Fourier representation of a complex wave of finite duration (as musical sounds are) requires an infinite number of different harmonics. Trying to represent actual sounds as sums of true sine waves, which persist from an infinite past into an infinite future, is a mathematical artifice.
Consider the nearly periodic sounds produced by musical instruments. A sum of harmonically related sine waves doesn't correctly represent such a sound, because the sound starts, persists a while and dies away.
"Noisy" sounds such as the hiss of escaping air or the "sh" or "s" sounds of speech can be represented as the sum of sine waves (a Fourier integral) that have slightly different frequencies. When the sound is repeated the waveforms won't be exactly the same. The power of the sound in any narrow range of frequencies will be about the same, but the amplitudes and phases of the individual frequency components won't be identical. Nevertheless the two different "sh" sounds will sound the same; we will hear them as being identical. It may however, for certain purposes, be adequate to use fewer components.
Rigden, John S. :Physics and the Sound of Music: J. Wiley 2nd ed.: 1985
Back to main course The Physics And Psychophysics Of Sound & Music
Back to Intensity
Next to Tuning, Scales And Temperament