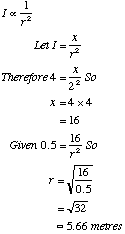), one must add 20 dB etc. Here are
some useful relations:
Working with Decibels
Whenever the intensity I is multiplied by a factor of 10, one just adds 10 dB
to the value of SL. When the intensity is multiplied by a 100 (10), one must add 20 dB etc. Here are
some useful relations:
2.2 Relationship between change in SL and I
There is a relationship between the intensity of a sine sound wave and the value
of the average pressure oscillation (
p) associated with the wave:
Where,
V = velocity of the sound wave
= the air
density
p = average
pressure oscillation.
For a sine wave, 
For normal conditions of temperature and pressure I = 0.00234 x (p) (watt/m). Since according to this relation I is proportional to
the square of p
(
) we
have
Hence, we can introduce the quality called sound pressure level (SPL):
Funny things seem to happen with the SPL when we superimpose two sounds of the same frequency and phase. According to the table above, doubling the intensity adds a mere 3 dB to the sound level of the original sound, whatever the actual value of the SL might have been. Superimposing ten equal tones in phase only increases the resulting SL by 10 dB.
To raise the SL of a given tone by 1 dB, we must multiply its intensity by 1.26 (or add a tone whose intensity is 0.26 that of the original).
Appendix A: Intensity/Distance Measurement Examples
1. If a sound is at an intensity of 0.5 watt/m at 20 metres from the source, what is the
intensity at
(a) 10 metres from the source.
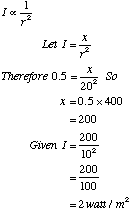
(b) 30 metres from the source.
Now x has the same value as (a) above because it is the same source.
2. If a sound is at an intensity of 2 watt/mat 3 metres from the source, what is the intensity at 1
metre from the source.
3. If a sound is at an intensity of 4 watt/m at 2 metres from the source, at what distance is it at
an intensity of 0.5 watt/m ?
