1. A lower limit - the threshold of hearing 10
Watt/m
= 0 dB, and
2. An upper limit - the threshold of pain 1 Watt/m = 120 dB.
The Psychophysics of Loudness
Review of Basic Concepts
Our ears are not at all interested in the total acoustical energy which reaches the
eardrum. They are, however, sensitive to the rate at which the energy arrives i.e.
the acoustical power (in Watts). This rate is what determines loudness.
Intensity, Sound Level, and Loudness
The amplitude of the eardrum oscillations leads to the sensation of loudness. This
amplitude is directly related to the average pressure variation Ip, of the incoming
sound wave and hence to the acoustical energy flow or intensity I reaching the ear.
There are two limits of sensitivity to a tone at a given frequency:
1. A lower limit - the threshold of hearing 10
2. An upper limit - the threshold of pain 1 Watt/m
These two limits vary from individual to individual and depend on the particular frequency under consideration. In general for a tone of 1 KHz the interval between limits is largest.
Because of the tremendous range, from 1 watt/m to 10 watt/m the unit of watt/m is impractical. The JND of a given stimulus is usually a good physical
"gauge" to take into account when it comes to choosing an appropriate unit
for the physical magnitude.
Experiments show that the JND in tone intensity is roughly proportional to the intensity of the tone. The magnitude used - the decibel - accomplishes three simultaneous objectives:
1. A compression of the whole audible intensity scale into a much smaller range of values,
2. The use of relative values (for example relative to the threshold of hearing) rather than absolute ones, and
3. The introduction of a more convenient unit whose value closely resembles the minimal perceptible change of sound intensity.
Firstly we adopt the threshold of hearing at 1 KHz of 10 Watt/m as our reference intensity 
. We can then calculate the relative quantity
Sound Intensity Level SL
SL = 10 log(I/)
(dB)
For the threshold of hearing I/ = 1 and SL = 0 dB.
For threshold of feeling I/ = 10
and SL = 10 x log 
12
= 120 dB.
Whenever the intensity I is multiplied by a factor of 10, one just adds 10 dB to the value of SL. When the intensity is multiplied by a 100, one must add 20 dB etc. Here are some useful relations:
There is a relationship between the intensity of a sine sound wave and the value of the average pressure oscillation associated with the wave.
p = average
pressure oscillation = pressure variation amplitude divided by 
, in Newton/m
V = velocity of the sound wave, and
= the air density.
For normal conditions of temperature and pressure I = 0.00234 x (p) (watt/m). Since according to this relation I is proportional to
the square of Ip, we have
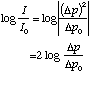
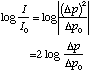
Hence, we can introduce the quality called sound pressure level:
Funny things seem to happen with the SPL when we superimpose two sounds of the same frequency and phase. According to the table above, doubling the intensity adds a mere 3 dB to the sound level of the original sound, whatever the actual value of the SL might have been. Superimposing ten equal tones in phase only increases the resulting SL by 10 dB.
To raise the SL of a given tone by 1 dB, we must multiply its intensity by 1.26 (or add a tone whose intensity is 0.26 that of the original).
The minimum change in SPL required to give a detectable change in the loudness sensation (JND in sound level) is roughly constant and of the order of 0.2 - 0.4 dB in the musically relevant range of pitch and loudness. Thus the unit of SPL or SL, the decibel, is thus reasonably close to the JND.
The perceived loudness of a sound, is however not directly proportional to its intensity. A built-in safety mechanism cuts down the sensitivity of the ear as intensity increases. When the intensity of a sound is doubled, the perceived loudness increases by only about 23%. Also, our perception of intensity varies with frequency - as we shall see later. Keeping frequency constant at say 1 KHz (1000 Hz),
| Intensity (watt/m) |
Perceived Loudness | SL (dB) |
|---|---|---|
| 1 | Threshold of Feeling | 120 |
| 10-3 | Extremely loud (fff) | 90 |
| 10-4 | Very loud (ff) | 80 |
| 10-5 | loud (f) | 70 |
| 10-6 | Moderately loud (mf) | 60 |
| 10-7 | Soft (p) | 50 |
| 10-8 | Very soft (pp) | 40 |
| 10-9 | Extremely soft (ppp) | 30 |
| 10-12 | Threshold of Hearing | 0 |
N.B. : THE INTENSITY AT THE THRESHOLD OF FEELING IS ONE TRILLION (10) TIMES GREATER THAN THE INTENSITY
AT THE THRESHOLD OF HEARING.