Intensity
Power in a Sound Wave
Sound originates when a vibrating source disturbs the air in a quasi-periodic fashion and sends a sound wave travelling through it. Another way of saying this is that a sound source radiates acoustical energy which is transferred to the medium (air) and this energy propagates through the air in the form of a sound wave.
Our ears are not very sensitive at all to the total acoustical energy which reaches them. They are however sensitive to the rate at which the energy arrives. This rate is what determines loudness. The rate at which an instrument radiates acoustical energy is the instrument's acoustic power output. (Power is the rate of doing work.) The unit of power is the watt1.
A musical instrument is a transformer. It is supplied with power by a performer or electricity. Much of this power is used to overcome friction/resistance and is "wasted" in other ways. Only a small proportion is transferred into musical sound. A pianist may use energy at the rate of 200 watts in a very loud passage without more than 0.4 watt being radiated as sound.
| Source | Power (watts) | Source | Power (watts) | |
| Orchestra (75 piece) @fff | 70 | Orchestra (75 piece) @mf | 0.09 | |
| Bass Drum | 25 | Piccolo | 0.08 | |
| Pipe Organ | 13 | Flute | 0.06 | |
| Snare Drum | 12 | Clarinet | 0.05 | |
| Cymbals | 10 | French Horn | 0.05 | |
| Trombone | 6 | Triangle | 0.05 | |
| Piano | 0.4 | Bass Voice | 0.03 | |
| Bass Saxophone | 0.3 | Alto Voice (pp) | 0.001 | |
| Bass Tuba | 0.2 | Average Speech2 | 0.000024 | |
| Double Bass | 0.16 | Violin (@pppp) | 0.0000038 | |
| Table 2.1. Power radiated as sound by various musical instruments (maximum loudness unless otherwise stated)+ | ||||
It can be observed from Table 2.1 above that the ratio of the of loudest to softest sounds is approx. 20,000,000 : 1. It can thus be appreciated that our ears are very sensitive to the rate at which energy arrives at the eardrum, i.e. they are sensitive to acoustical power. It is the amplitude of the eardrum oscillations which leads to the sensation of loudness and this amplitude is directly related to the average pressure variation *p, of the incoming sound wave.
Definition of Intensity
The intensity (or energy flow) of a sound wave is the power (in energy/sec) transmitted through an area of 1m
oriented perpendicular to (normal to) the propagation direction of the wave3.
Almost everyone knows that if they move away from a constant sound source, they perceive a decrease in loudness. Consider the following example:
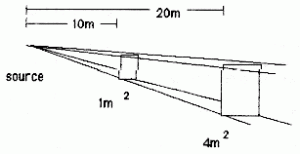
Assume that a sound from a source propagates through 1m of air at 10m from the source. Looking at the diagram we can see that the power that is concentrated over 1m at 10m from the source, is spread over a larger area at the distance of 20m. The same amount of energy is spread over a larger area, so the intensity has decreased. Specifically, the area at 20m is 4m which is 4 times the area at 10m (1m), making the energy at 20m 1/4 the intensity that it was at 10m. That is:
where r is the distance from the source.
The sensation of loudness is determined by the intensity. The greater the intensity the greater is the perceived loudness. It is usual to symbolise intensity as I expressed in watt/m.
Human hearing falls roughly in the range 1 Watt/m (the loudest, called the Threshold of Feeling) to 10
Watt/m (the softest, called the Threshold of Hearing. 10 = 0.000000000001 . (12 decades.)
These two thresholds vary from individual to individual and depend on the particular frequency under consideration. The size of this range is tremendous ( a trillion values); The unit of watt/m produces very unwieldy numbers. For these reason and others, the units watt/m is impractical.
Sound Intensity Level (SL)
These size-of-domain difficulties are avoided if we use a logarithmic scale based on a ratio of intensities. As it happens, we are normally more interested in comparing intensities than dealing with absolute values. This comparison is achieved by observing their ratio. For example, if the ratio of the intensities of two sounds is 3, one intensity is thrice that of the other.
Instead of specifying the power density (intensity) itself it is customary to specify how many times the actual power is greater than the power of a reference-level soundwave. This reference level is
10 Watt/m. This is about the weakest sound that humans can hear. The intensity of a sound above this reference level is the Sound Intensity Level(SL) of the sound.
If one sound has an intensity 
( in Watt/m) and a second sound has an intensity 
, the second has an intensity relative to the first of /. The log
of this ratio gives us a value for the relationship, the unit being the bel after Alexander Graham Bell, the inventor of the telephone.
Definition: 
The human audible range is then 
A still more practical unit of sound intensity level, SL, that is used more widely today, is the tenth part of a bel, the decibel (dB).
where = 10 Watt/m, the intensity at the threshold of hearing. functions as a reference intensity - i.e. larger intensities are compared to through the ratio /.
Calculation of some useful Sound Levels (SL's, in decibels)
1. Threshold of Feeling - SL of I = 
N.B. The scale of SL's has been compressed from between 10 watt/mand 1 watt/mto between 0 and 120 dB - which is much more convenient.
2. Threshold of Hearing - SL of I = 10 watt/m
3. "Fortissimo" - SL of I = 10
watt/m
4. "Pianissimo" - SL of I = 10
watt/m
5. Doubling The Sound Intensity Level
What is the change in SL when the intensity, I, is doubled?
Sound Intensity Level and Distance
If a sound is not reflected or interrupted, the intensity drops 6 dB ( i.e. 0.25 of its value) every time we double the distance. Thus, if the SL is 90 dB at 2 metres from the source, it will be 84 dB at 4 metres and 78 dB at 8 metres.
Working with Decibels
Whenever the intensity I is multiplied by a factor of 10, one just adds 10 dB to the value of SL. When the intensity is multiplied by a 100 (10), one must add 20 dB etc. Here are some useful relations:
| Change in SL | What Happens to the Intensity | |
| =(-) 1 bd | x (div) by | 1.26 |
| =(-) 3 bd | x (div) by | 2 |
| =(-) 10 bd | x (div) by | 10 |
| =(-) 20 bd | x (div) by | 100 |
| =(-) 20 bd | x (div) by | 1000000 |
| 2.2 Relationship between change in SL and I | ||
There is a relationship between the intensity of a sine sound wave and the value of the average pressure oscillation (
p) associated with the wave:
Where,
V = velocity of the sound wave
= the air density
p = average pressure oscillation.
For a sine wave, 
For normal conditions of temperature and pressure I = 0.00234 x (p) (watt/m). Since according to this relation I is proportional to the square of p (
) we have
Hence, we can introduce the quality called sound pressure level (SPL):
Funny things seem to happen with the SPL when we superimpose two sounds of the same frequency and phase. According to the table above, doubling the intensity adds a mere 3 dB to the sound level of the original sound, whatever the actual value of the SL might have been. Superimposing ten equal tones in phase only increases the resulting SL by 10 dB.
To raise the SL of a given tone by 1 dB, we must multiply its intensity by 1.26 (or add a tone whose intensity is 0.26 that of the original).
Appendix A: Intensity/Distance Measurement Examples
1. If a sound is at an intensity of 0.5 watt/m at 20 metres from the source, what is the intensity at
(a) 10 metres from the source.
(b) 30 metres from the source.
Now x has the same value as (a) above because it is the same source.
2. If a sound is at an intensity of 2 watt/mat 3 metres from the source, what is the intensity at 1 metre from the source.
3. If a sound is at an intensity of 4 watt/m at 2 metres from the source, at what distance is it at an intensity of 0.5 watt/m ?
A Review of Logarithms
The logarithm to the base 10 of a number is the exponent to which 10 must be raised, to yield that number. e.g. 100 =10 therefore 2 = log100. Here are some other examples:
| 1000 = 103 > log101000 = 3 1000 = 101 > log1010 = 1 1000 = 100 > log101 = 0 1000 = 10-1 > log100.1 = -1 1000 = 10-2 > log100.01 = -2 |
| Number | log10 of Number (3 decimal places) |
| 1 | 0 |
| 2 | 0.301 |
| 3 | 0.477 |
| 4 | 0.602 |
| 5 | 0.699 |
| 6 | 0.778 |
| 7 | 0.845 |
| 8 | 0.903 |
| 9 | 0.954 |
| 10 | 1.000 |
| Logarithms (base 10) of numbers between 1 and 10 | |
Comparison of Sound Intensity Level (SL) and Sound Pressure Level (SPL)
SL = 10 x log (I/) where I is the intensity in watts/m. The unit is decibel, denoted "dB". For the hearing threshold, I/ = 1 and SL = 0 dB. For the feeling threshold, I/ = 10
= 120 dB.
Note that when a quantity is expressed in decibels a relative measure is given. That is, it is given with respect to some reference value ( in the case of SL). Whenever the intensity (I) is multiplied by a factor of 10, one just adds ten decibels to the value of SL. Whenever the intensity is multiplied by a factor of 100, one just adds 20 decibels to the value of SL.
Now, there is a relation between the intensity of a sine sound wave (I) and the value of the average pressure variation Dp. (Dp= pressure variation amplitude divided by 2.) 
where V is the velocity of sound in air and is the air density. For normal conditions of air and temperature,
I = 0.00234 x Dp. Dp is in Newton/m .
Now the threshold of hearing is 10 watt/m. According to this expression for I above, this represents an average pressure variation of only 2.0 x 10
Newton/m.
This relation also shows that I is proportional to the square of Dp, thus 
Thus the quantity Sound Pressure Level (SPL):
SPL = 20 log 
.
For a travelling wave, the numerical values of SL and SPL are identical and SPL and SL are one and the same thing.
Now, for standing waves, there is no energy flow at all and the intensity I cannot be defined, hence SL loses its meaning. Yet the concept of average pressure variation Dp at a given point in space (at the entrance to the auditory canal for example) remains meaningful. That is why SPL is more frequently used than SL.
1 1 watt is the power required to raise 0.45 Kg 215 mm/sec (approx.) A man doing hard continuous labour develops about 100 watts - the power required to keep a 100W electric light bulb burning.
2 It would take thus approximately 2 million people in conversation to keep a 50 Watt electric light blub burning.
3 The energy flow associated with a sound wave is the total mechanical energy (potential and kinetic energies associated with elastic oscillations of the medium) that is transferred during each second through a surface of unit area (1m) - expressed in Joule/m/sec or Watt/m. This is commonly called the intensity of the wave and is designated I.
+ Wood, A : The physics of music: Methuen London 6th ed. : 1962
Back to main course The Physics And Psychophysics Of Sound & Music
Back to Frequency Of A Sound Wave
Next to Spectra