Introduction To The Psychophysics of Hearing*
JND - Just Noticeable Difference
There is a natural limit to an individuals ability to establish a relative order of pitch when two pure tones (sine tones) of the same intensity are presented one after another. When the difference in frequency between the two tones is too small, both tones are judged as having the same pitch. This is true for order judgments for all psychophysical magnitudes: whenever the variation of an original physical stimulus lies within a certain difference limen or just noticeable difference (JND) the associated sensation is judged as remaining the same. As soon as the variation exceeds the JND, a change in sensation is detected.
Frequency and Pitch
The degree of sensitivity of the primary pitch mechanism to frequency changes (frequency resolution capability) depends on the frequency, intensity, and duration of the tone in question. It varies greatly from person to person, is affected by musical training, and depends considerably on the method of measurement employed.
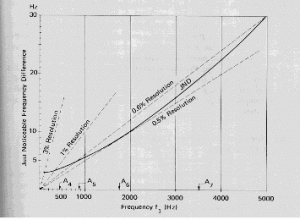
Figure 2.9 shows the average JND in frequency for pure tones of constant intensity (80 dB) whose frequency was slowly and continuously modulated up and down. The graph shows, for example that for a tone of 2 KHz a change of 10 Hz (ie only 0.5%) can already be detected. This is a very small fraction of a semitone!. Sudden changes are detected with a considerably lower JND (up to 30 times smaller than the values shown).
The JND in frequency is not defined sharply. There are two critical thresholds:
- A frequency increment below which a change in pitch is never detected, sometimes called the neural quantum of pitch detection; and
- A frequency increment above which a change in pitch is always detected, the value of which is approximately twice that of the neural quantum.
Psychophysics of Pitch Perception
Superimposition of Pure Tones: First Order Beats and the Critical Band
In this section we will analyse the fundamental characteristics of the superimposition of two sine tones. In doing so we will come across some very fundamental concepts of the physics and psychophysics of music.
There are two sorts of superimposition effects, depending on where they are processed in the listeners auditory system:
- First order superimposition effects: in which the processing is mechanical, ie in the cochlear fluid and along the basilar membrane.
- Second order superimposition effects are the result of neural processing. These are much more difficult to detect, describe and measure unambiguously. We shall focus on first order effects.
The Physical Meaning of "Superposition of Sound"
The Eardrum moves in and out in response to pressure variations of the air in the auditory canal. If it oscillates in pure simple harmonic motion of a given frequency and amplitude, we hear a sine tone of a certain pitch and loudness. If two such tones of different characteristics are sounded together the auditory system reacts as if the eardrum was receiving two independent commands simultaneously, one given by each sine tone.
Provided that the amplitudes are not too large, the resulting motion of the eardrum (and all the other vibrating components) is the sum of the individual motions that would occur if each tone were presented alone, in the absence of the other. This characteristic is called a linear superposition of two vibrations.
Superimposition of two sine tones of equal frequency and equal phase.
The superimposition of two sine tones of equal frequency and equal phase results in a sine tone of the same frequency and the same phase, but whose amplitude is the sum of the amplitudes of the two component vibrations.
If the two component vibrations have different phases, their superimposition is still a sine tone of the same frequency, but the amplitude will be the sum of their amplitudes in time. In particular, if the phase difference is 180deg. both oscillations will annihilate each other and no sound will be heard. This is called destructive interference and plays a role in room acoustics.
Superimposition of two sine tones (y1 and y2 ) of equal amplitude with slightly different frequencies.
freq y1 = f1 freq y2 = f2
Assume f2 = f1 + 
f such that the frequency difference f has a small absolute value.
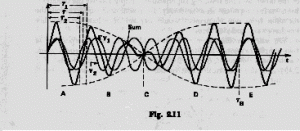
The vibration pattern of the eardrum is still the same as before, namely the sum of the pattern of each component tone.
Note:
- The slowly changing phase difference between the component tones y1 and y2. They start in phase (0deg. phase difference) at the instant t=0, then y2 starts leading y1 in phase, until both are completely out of phase (180deg. phase difference). The phase difference keeps increasing until it reaches 360deg. = 0deg. at instant tB.
- This continuous slow phase shift is responsible for the changing amplitude of the resultant oscillation which is represented by the broken line curves.
Sensation of the superposition of two tones
Note that the eardrum will follow the oscillation prescribed by the heavy curve ( the sum of y1 and y2). It does not "know" that this pattern is the result of two others.
This more complicated but single vibration pattern (the summation tone) arrives at the oval window and gives rise to two groups of travelling waves in the cochlear fluid, one for each of the component tones!! If the frequency difference f between the two component tones is large enough, the corresponding resonance regions of the basilar membrane are sufficiently separated from each other for each of these regions to oscillate with a frequency corresponding to a component tone and we thus hear two separate tones of constant loudness with pitches corresponding to each of the original tones.
This property of the cochlea disentangling a complex vibration pattern into original tone components is called frequency discrimination. It is a mechanical process, controlled by the hydrodynamic and elastic properties of the inner ear constituents.
If however, the frequency difference f is smaller than a certain amount, the resonance regions of the basilar membrane overlap and we hear only one tone of intermediate pitch with modulated or beating loudness. In this case the overlapping region of the basilar membrane follows a vibration pattern essentially identical to that of the eardrum. The amplitude modulation of the perceived pattern (broken curve) causes the perceived loudness modulation. This is called first order beats.
The frequency of the resulting vibration pattern, fr is equal to the average value:
The time interval Trafter which the resulting amplitude attains the initial value is called the beat period. The beat frequency fB = 1/TB turns out to be given by the absolute value of the difference in the two frequencies:
fB = <<f2+ f1<< = f
The closer together the frequencies f1 and f2 are the "slower" the beats will be.
What Happens When 
fD approaches fCR
In summary then, When f surpasses the so called limit of frequency discrimination fD, we distinguish two separate tones. However at that limit the sensation of roughness still persists, especially in the low pitch range. Do not confuse fD with the limen of frequency discrimination, the JND for pitch.
Only after surpassing a still larger frequency difference fCR called the critical band, the roughness sensation disappears and both tones sound smooth. This transition from roughness to smoothness is gradual.
Limits
The limits for pitch discrimination and the critical band depend strongly on the centre frequency (the average frequency 
of the two tone stimuli. They are both relatively independent of amplitude, but may vary considerably from individual to individual.
The critical band is related to several psychoacoustical phenomena. The following figure shows the dependence of pitch discrimination fD and critical band fCR with the centre frequency of the component tones.
From this graph we can see for instance that two tones in the region of 2 KHz must be at least 200 Hz apart to be discriminated, and more than 300 Hz apart to sound "smoothly".
Notes
- That the limit of pitch discrimination is larger than a 1/2 tone and even larger than a whole tone at both audio frequency extremes.
- That in the higher frequency range the critical band lies between the frequency difference that corresponds to a whole tone ( dissonance) and that of a minor third (consonance) i.e. roughly extending over 1/3 of an octave.
- In the lower frequency range frequency discrimination and critical band are larger than a minor third (and even a major third). This is why intervals of thirds in general are not used in the deep bass register in tonal music.
- In comparing figure 2.13 with 2.9 the limit for frequency discrimination fD is roughly 30 times larger than the JND for frequency resolution. i.e we can detect very minute frequency changes in a single sine tone, but it takes an appreciable frequency difference between two pure tones sounding simultaneously to hear out each component separately.
- When each one of the two tones f1 and f2 is fed binaurally into a different ear the primary beat or roughness sensation disappears at once and both tones can be discriminated even if the frequency difference is way below fD. When we switch back to monaural input the beats or roughness come back. What is happening in the binaural case is that there is only one activated region of each basilar membrane with no chance for overlapping signals in the cochlea.
The experimental fact that the critical band frequency extension fCD is roughly speaking independent of loudness is a strong indication that it must be related to some inherent property of the organ of Corti on the basilar membrane rather than the waveform in the cochlear fluid.
By converting this frequency extension fCB into spatial extension along the basilar membrane (using fig 2.8) we can see that the critical band fCB is an almost constant value of approximately 1.2 mm. Also, this section of basilar membrane is "serviced" by a roughly constant number of about 1,300 (out of 30,000) receptor cells independently of any particular centre frequency (i.e. independent of the position on the membrane.)
Combination Tones
Combination tones sometimes result when two tones are sounded together#. For example, when the frequency of a frequency variable sine tone fvar increases beyond the critical band from a unison position with a fixed sine tone ffixed, additional pitch sensations appear. They are most easily perceived at high intensity levels. These pitches are not present in the original sound stimulus - they appear as the result of a so-called non linear distortion of the acoustical signal in the ear. They are not present at the oval window membrane but are thought to be caused by the non-linear response of the cochlea. We say that the cochlea produces a non-linear or distorted response.
It can be shown experimentally that sweeping the frequency of fvar slowly upwards from the unison at ffixed to an octave above at 2ffixed causes pitch sensations other than these two tones. As fvar sweeps upwards away from ffixed one or more lower pitched rising tones are perceived. As fvar approaches 2ffixed (the octave) the lower tones "disappear".
The most easily perceived of these combination tones is the one whose frequency is given by the difference of the component frequencies:
fc1 = fvar- ffixed called the difference tone.
For fvar close to ffixed the difference tone is nothing but the beat frequency. fc1 must be at least 20-30 Hz to be heard as a tone. As fvar increases fc1 increases until when fvar= 2ffixed (ie an octave above) , then
fc1= 2ffixed - ffixed= ffixed.
That is, the frequency of the difference tone coincides with the frequency of the lower component ffixed.
When fvar is half way between ffixed and 2ffixed ,i.e. fvar = 3/2 (ffixed) ( a pure perfect fifth), then the difference tone has a frequency:
fc1 = (3/2)ffixed - ffixed
= (1/2)ffixed
which corresponds to the frequency of a tone one octave below ffixed.
The two other tones most easily identifiable correspond to the frequencies
fc2 = 2ffixed - fvar , and
fc3 = 3ffixed - 2fvar
Their "pitch paths" both decrease as fvar increases from the unison towards the fifth.
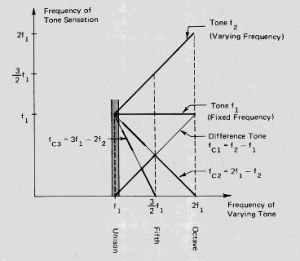
Note that the frequencies of fc1and fc2 coincide (=1/2 ffixed) at the fifth - when fvar = 3/2 ffx. (see below for summary.)
Note again that this is a "close-up" mapping of what happens with beat frequencies.
Extension Topics
Second Order Effects:
- Beats of Mistuned Consonances
- Fundamental Tracking
- Periodicity Pitch and the Theory of Hearing
* Main Reference: Roederer, Juan : Introduction to the Physics and Psychophysics of Music: The English Universities Press, London 1973.
# This effect is not to be confused with the additional pitch sensations perceived when a single tone is played very loudly. These additional tones are called aural harmonics and their frequencies correspond to integer multiples of the frequency of the single tone in question.
Rigden, John S. :Physics and the Sound of Music: J. Wiley 2nd ed.: 1985
Back to main course The Physics And Psychophysics Of Sound & Music
Back to The Physiology of Hearing
Next to The Psychophysics of Loudness